Instructions for the Computational Project [50/100 points]
- The computational project counts up to a 50% of the total score (50/100 points)
- The project gives you the possibility to work independently on a medium-level topic of Computational Plasma Physics
- The project will be individual, no group projects will be accepted
- The goal of the project is twofold:
- (Goal A) Make practice preparing good scientific papers: this will always be required in your professional life, either in the form of technical reports, or in the form of scientific publications
- (Goal B) Make practice presenting your scientific work, like at conferences
- The computational project is made of 2 parts:
- (1) Written report & code [40/100 points]
- (2) Oral presentation [10/100 points]
- The written report will be a concise but detailed description of the scientific activity that you have done. The technical content will have to be minimum 1500 words (roughly 5 pages), plus the references, and the pages reporting the code produced. The references and the code will not count toward the total number of words, but they will have to be included in the report. The grading of the written report will be based on the following sections of the document: title, abstract, introduction and literature review, model derivation, model discretization, implementation, numerical analysis, production runs, scientific results, conclusions, references, and code produced. Furthermore the overall scientific quality, the coding quality, clarity, and style, and the technical writing will also be considered in the evaluation process. The written report is due one week before the oral presentations, on
December 7, 2016, 1:30 PM. Extended to: December 8, 2016, 1:30 PM. - The oral presentations will be on Wednesday, December 14, 1:30-4:30pm (http://registrar.illinois.edu/fall2016schedulingguidelinesfaculty_staff). Presentations will be of 10 minutes per person, plus ~4-5 minutes for discussions and questions.
Progress Monitoring
An early start of the computational project is strongly encouraged! Even if the project will be graded only at the very end of the course, I will monitor the progress of your project along the semester. You should stay on track with the schedule reported below.
- Week 1-3: start thinking about the topic you prefer for your project
- By End of Week 3: write me an email with the topic you would like to address
- End of Week 3/Beginning Week 4 (in class): preliminary discussion and directions on the projects
- Week 4-6: Literature search and model development (which equations describe your system?)
- Week 7-9: Model discretization
- By End of Week 9: produce a first draft of the project, with the overall structure, the literature search, model description, and model discretization. The first draft will not be graded, but I will want to see it, because it will offer the possibility to discuss on possible early adjustments and on the following important step of model implementation.
- Week 10-12: Implementation
- By End of Week 12: Second draft of the project: software review. The project will not be graded at this point. This second project review gives me the possibility to monitor how the code implementation is proceeding, and eventually give directions, suggestions, etc.
- Week 13-15: Numerical Analysis and/or Production Runs
- Week 16: Complete the report
- Dec 7, 2016, 1:30 PM: Due date of the Computational Project
- Dec 7-14, 2016, 1:30 PM: Final Review of the Computational Projects
- Dec 14, 2016, 1:30-4:30 PM: Oral presentations
Few selected past projects NPRE 498-Numerical Methods
- Dispersion Modes and Numerical Stability of a Cold Unmagnetized Plasma analyzed via Particle Methods. [G. Panici] Analysis of Langmuir oscillations using a particle-mesh method. Comparison with analytical predictions of small oscillations. Identification of how different particle models affect the results. Characterization of the stability regions.
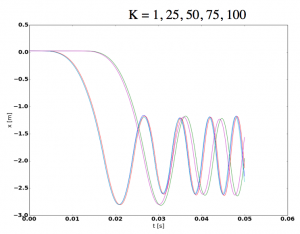
- Dispersion Modes and Numerical Stability of Hybrid Oscillations analyzed via Particle-Mesh Methods. Analysis of Hybrid oscillations using a particle-mesh method. Comparison with analytical predictions for small oscillations (cold theory). Identification of how different particle models affect the results. Characterization of the stability regions.
- Two Stream Instability analyzed via Particle-Mesh Methods. [F. Bedoya] Linearized dispersion relation of a plasma made of two opposing streams. Particle simulations of the two-stream instability. Measurements of the growth rate and oscillation frequencies, and comparison with the linear theory. Characterization of the non-linear features: peak values of the charge density, thickness of bunches, ratio of potential energy at saturation and initial kinetic energy, trends of the growth rate, decrease in the streaming velocity with consequent increase in velocity spread.
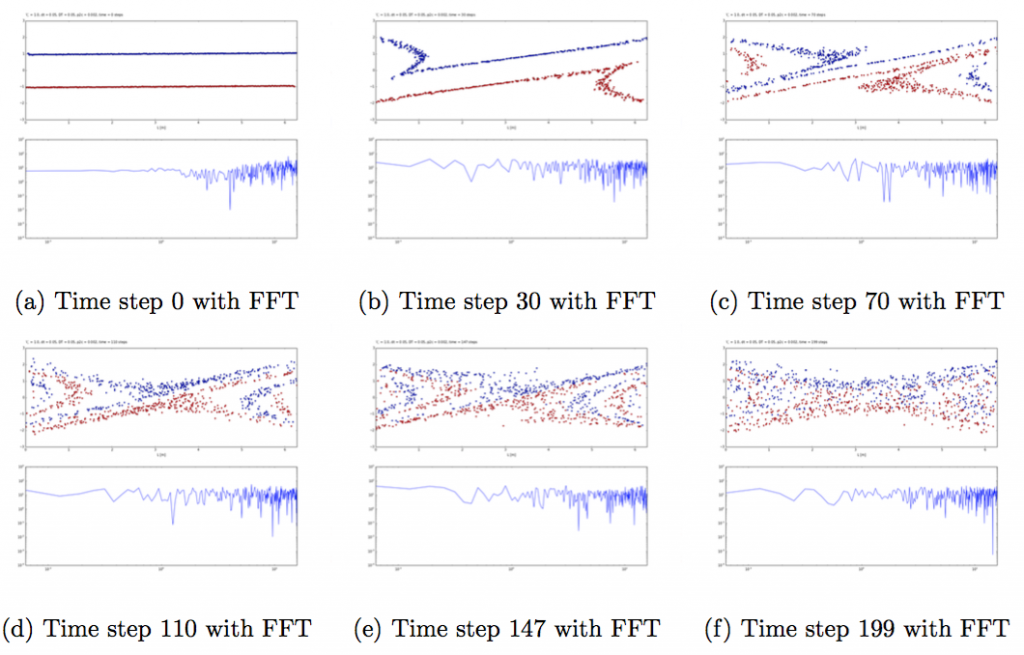
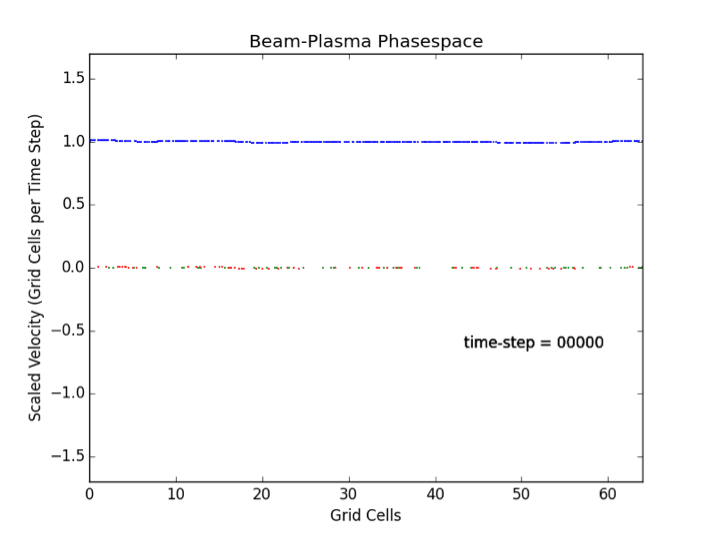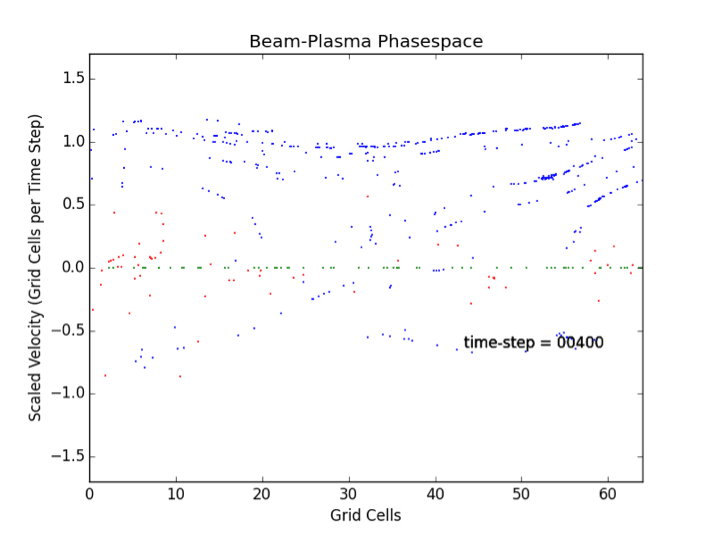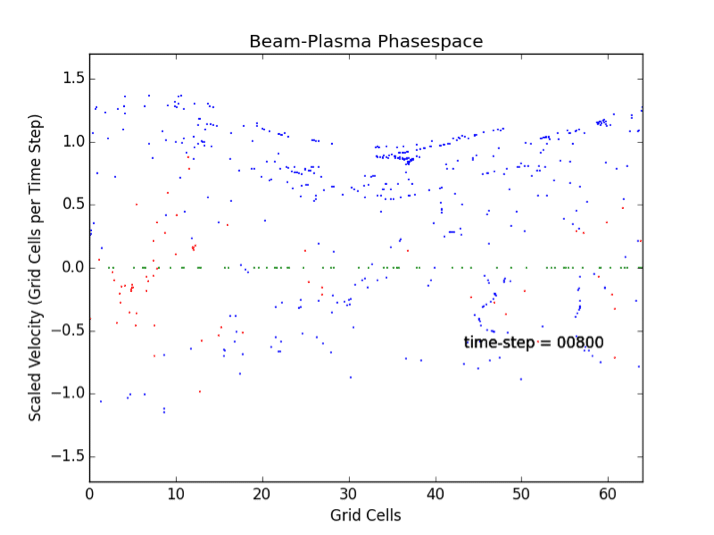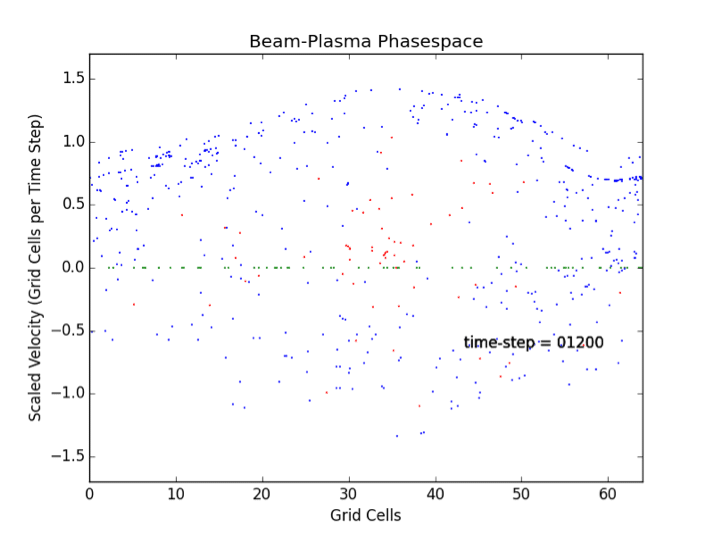
- Beam Plasma Instability analyzed via Particle-Mesh Methods. [K. Gimbel] This project deals with the analysis of a fast beam injected in a stationary plasma. Linearized dispersion relation of the beam-plasma problem. Particle simulations. Measurements of the growth rate and oscillation frequencies, and comparison with the linear theory. Characterization of the non-linear features: peak values of the charge density, thickness of bunches, ratio of potential energy at saturation and initial kinetic energy, trends of the growth rate and growth saturation.
- Beam Cyclotron Instability analyzed via Particle-Mesh Methods. The relative E×B drift of ions through electrons causes a special case of a two-stream instability relevant for plasma heating using low frequency electric fields.
- Landau Damping analyzed via Particle-Mesh Methods. Well, the title is self explanatory.
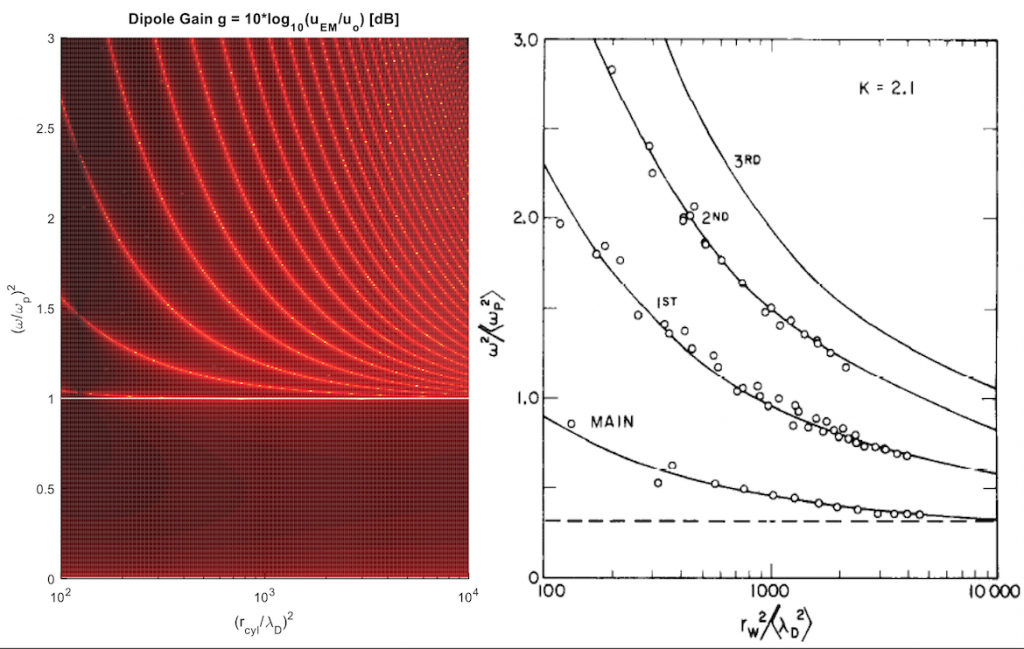
- A study on the Electromagnetic Scattering of a Plasma Column: the problem of Plasma Antennas. [J. Peck] An electromagnetic wave of wavelength λ incident on a uniform unmagnetized plasma column of radius a (with λ ≫ a) is scattered by the column with a spectrum exhibiting a number of resonances called the Tonks-Dattner resonances. In the cold-plasma approximation a zero-th order description of the resonances can be done simply solving an opportune Laplace equation of the oscillating potential inside and outside the column. The solution exhibits a scattering of dipole nature. After defining the model of the problem, solve the resulting Laplace equation analytically first, and then numerically by discretizing the Laplace using finite differences. Calculate the resonance frequencies, and compare the analytical vs. the numerical solutions of the resonant frequencies. The resonances calculated in this way do not account for the multiple resonances observed in the experiments. The inclusion of finite-temperature effects is required for a better (still incomplete) representation of the scattering. At the lowest order, the Bohm-Gross thermal correction to the cold unmagnetized plasma allows a better (still wrong) estimate of the multiple resonances. The corresponding model involves a 4th order PDE of the electrostatic potential, that can be decomposed into a Laplace problem and an Helmholtz problem. Write a discretization of the Helmholtz problem, and compare the calculated quantities with Gould’s analytical solution (1959). Finally, consider the inclusion of plasma inhomogeneities. A satisfactory model can only be obtained by including the actual inhomogeneous density profiles of the finite-temperature plasma column, as numerically done by Parker in 1964. [Parker, Nickel, and Gould, Phys. Fluids 7 1489 (1964)].
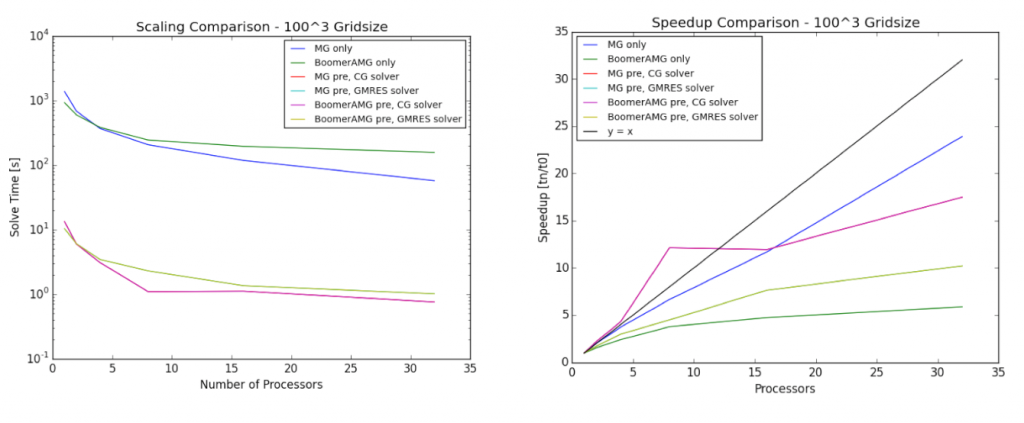
- Fast Elliptic Solvers for Particle-in-Cells. [S. Keniley] Comparison of performance of spectral methods versus finite-difference methods. This project focuses on the performance analysis of efficient elliptic solvers. Fast elliptic solvers are necessary for the solution of non-linear Poisson problems in electrostatic codes. FFTW is a famous C subroutine library for computing the discrete Fourier transform (DFT) in one or more dimensions, of arbitrary input size, and of both real and complex data.
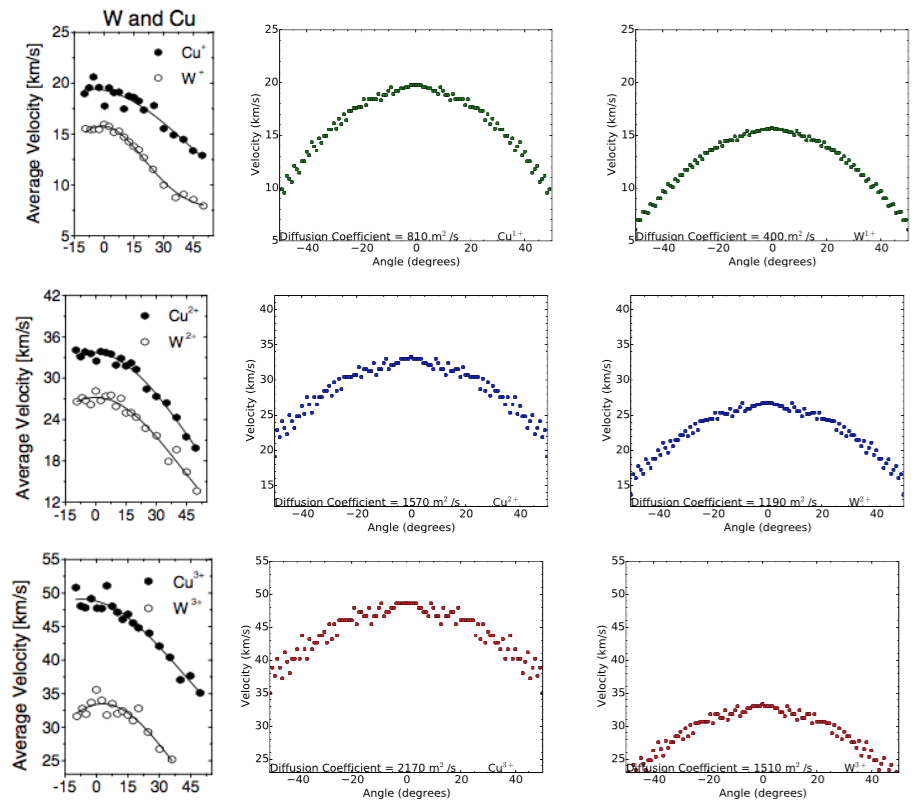
- Application of an Advection-Diffusion Model to Laser Ablation and Comparison to Experimental Results. [N. Walter] Laser ablation, the process of removing material from a surface by irradiation with a laser, is a rapidly growing asset in many manufacturing fields. However, the timescale and length scale of the ablation process ranges from picoseconds on the atomistic scale to seconds on the continuum scale making the entire ablation process difficult to model in entirety. In this report we attempt to accurately model the plume development as a 2-D advection-diffusion process. The simulation results are in placed in contrast to the experimental results of [16], which studied the velocities of copper and tungsten ions as a function of angle from the normal. By comparing simulations to experiments, we determine the extent the diffusion-advection process models the physics of plume development after irradiation. The experimental setup used in [16] is reproduced and simulated. The advection-diffusion process is shown to crudely reproduce the results of [16], however, elements of the complete plume development process are absent when using the advection-diffusion model.
- Propose your project. I am open for discussion on a final project of your choice, different than those reported in this list.